![[自拍偷拍]藝校美女孔雀妹妹三人組同時表演才藝 数学也能很道理: 全国十大烧脑数学难题](/uploads/allimg/250701/011219130104519.jpg)
数学,这门陈腐而巧妙的学科,自古以来就以其独有的魔力诱骗着无数的学者和爱好者。然则,数学的全国并非一派坦途,其中存在着好多令东说念主视为畏途的难题,这些难题如同望尘莫及的山岭,挑战着东说念主类的灵巧极限。今天[自拍偷拍]藝校美女孔雀妹妹三人組同時表演才藝,就让咱们一同走进这些全国数学难题的全国,感受它们的巧妙与魔力。
1. 哥德巴赫猜思
哥德巴赫猜思是数学家哥德巴赫于1742年提议的,它猜思任何一个大于2的偶数齐不错暗示为两个质数之和。尽管经过了数百年的接头,这一猜思于今仍未得到解释,也未被推翻,它如归并颗灿艳的明珠,诱骗着无数数学家为之立志。

2. 黎曼猜思
黎曼猜思是对于复分析中黎曼ζ函数的零点散布的猜思。它指出,黎曼ζ函数的统统非无为零点齐位于复平面上的临界线上。这一猜思对于数论的发展具有极其勤奋的深嗜深嗜,然则,尽管无数数学家为之致力,黎曼猜思于今仍然是一个未解之谜。

3. 费马大定理
费马大定理是法国数学家费马在1637年提议的一个猜思,它指出当整数n>2时,对于x、y、z的方程x^n+y^n=z^n莫得正整数解。这个看似节略的猜思,却困扰了数学家们300多年,直到1994年,英国数学家安德鲁·怀尔斯才最终解释了这一定理,为这一长达三个多世纪的数学难题画上了句号。

4. 四色定理
四色定理是一个着名的图论问题[自拍偷拍]藝校美女孔雀妹妹三人組同時表演才藝,它猜思任何平面舆图齐不错只用四种神色来染色,使得相邻的区域神色不同。这一猜思在1976年被好意思国数学家阿佩尔和哈肯借助策画机解释,黑丝袜的诱惑然则,由于其解释经过复杂且依赖于策画机,这一解释在数学界仍然存在一定的争议。

5. 庞加莱猜思
庞加莱猜思是法国数学家庞加莱于1904年提议的一个拓扑学猜思,它指出任何一个单连通的三维闭流形齐同胚于三维球面。这一猜思在2006年被俄罗斯数学家佩雷尔曼解释,他因此得到了菲尔兹奖,但他却拒却了这一荣誉。

6. P vs NP问题
P vs NP问题是策画机科学中的一个中枢问题,它琢磨的是详情趣多项式技能可解的问题(P类问题)与非详情趣多项式技能可解的问题(NP类问题)之间的干系。这一问题于今仍未得到处罚,它对于策画机科学的发展具有极其勤奋的深嗜深嗜。

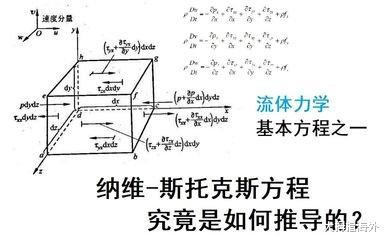
7. 纳维-斯托克斯方程
尤物皇后纳维-斯托克斯方程是流膂力学中的一个基本方程,它形容了粘性不能压缩流体的指点。然则,这一方程的解的存在性与独一性于今仍然是一个未解之谜,它对于清晰流体的指点具有极其勤奋的深嗜深嗜。
8. 贝赫和斯维讷通-戴尔猜思
贝赫和斯维讷通-戴尔猜思是对于椭圆弧线的有理点的猜思,它指出椭圆弧线的有理点的个数与椭圆弧线的某个算术不变量推测。这一猜思对于数论的发展具有极其勤奋的深嗜深嗜,然则,它于今仍未得到解释。

9. 霍奇猜思
霍奇猜思是对于代数几何中的霍奇类的猜思,它指出代数簇上的霍奇类齐是代数的。这一猜思对于代数几何的发展具有极其勤奋的深嗜深嗜,然则,它于今仍未得到解释。

10. 阿贝尔群的分类问题
阿贝尔群的分类问题是代数中的一个经典问题,它琢磨的是若何对统统有限生成的阿贝尔群进行分类。尽管这一问题在一定进程上得到了处罚,但其完好的分类仍然是一个未解之谜,它对于代数的发展具有极其勤奋的深嗜深嗜。

这些数学难题如归并座座峻岭,挑战着东说念主类的灵巧极限。尽管许巨额学家为之立志,但这些难题于今仍未被统统攻克。它们的存在不仅鼓吹了数学的发展,也激勉了无数东说念主对数学的把稳与追求。如若你对这些数学难题感兴致,不妨潜入接头,说不定你便是阿谁解开谜团的英杰!
PS:部分图文来自网路[自拍偷拍]藝校美女孔雀妹妹三人組同時表演才藝,侵删!
上一篇:ady映画 北交所上市公司好意思心翼申登龙虎榜: 当日换手率达到46.64%
下一篇:没有了
